Is AnyOne Good with Integers!!

Ohio
United States
Member #50440
February 21, 2007
25496 Posts
Online

Posted: April 30, 2012, 7:20 pm - IP Logged

Quote: Originally posted by CajunWin4 on April 30, 2012

The integers(from the Latin integer, literally "untouched", hence "whole": the word entire comes from the same origin, but via French^[1]) are formed by the natural numbers (including 0) (0, 1, 2, 3, ...) together with the negatives of the non-zero natural numbers (−1, −2, −3, ...). Viewed as a subset of the real numbers, they are numbers that can be written without a fractional or decimal component, and fall within the set {..., −2, −1, 0, 1, 2, ...}. For example, 21, 4, and −2048 are integers; 9.75, 5½, and √2 are not integers.

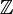The set of all integers is often denoted by a boldface Z (or blackboard bold $\mathbb{Z}$ , Unicode U+2124 Z), which stands for Zahlen (German for numbers, pronounced ['tsa?l?n]).^[2]

The integers (with addition as operation) form the smallest group containing the additive monoid of the natural numbers. Like the natural numbers, the integers form a countably infinite set.

In algebraic number theory, these commonly understood integers, embedded in the field of rational numbers, are referred to as rational integers to distinguish them from the more broadly defined algebraic integers.

The integers can be formally constructed as the equivalence classes of ordered pairs of natural numbers (a, b).^[3]

The intuition is that (a, b) stands for the result of subtracting bfrom a.^[3] To confirm our expectation that 1 − 2 and 4 − 5 denote the same number, we define an equivalence relation ~ on these pairs with the following rule:

$(a,b) \sim (c,d) \,\!$

precisely when

$a+d = b+c. \,\!$

Addition and multiplication of integers can be defined in terms of the equivalent operations on the natural numbers^[3]; denoting by [(a,b)] the equivalence class having (a,b) as a member, one has:

$[(a,b)]+[(c,d)] := [(a+c,b+d)].\,$ $[(a,b)]\cdot[(c,d)] := [(ac+bd,ad+bc)].\,$

The negation (or additive inverse) of an integer is obtained by reversing the order of the pair:

$-[(a,b)] := [(b,a)].\,$

Hence subtraction can be defined as the addition of the additive inverse:

$[(a,b)]-[(c,d)] := [(a+d,b+c)].\,$

The standard ordering on the integers is given by:

$[(a,b)]<[(c,d)]\,$ iff $a+d < b+c.\,$

It is easily verified that these definitions are independent of the choice of representatives of the equivalence classes.

Every equivalence class has a unique member that is of the form (n,0) or (0,n) (or both at once). The natural number nis identified with the class [(n,0)] (in other words the natural numbers are embedded into the integers by map sending n to [(n,0)]), and the class [(0,n)] is denoted −n (this covers all remaining classes, and gives the class [(0,0)] a second time since −0 = 0.^{[citation needed]}

Thus, [(a,b)] is denoted by^{[citation needed]}

$\begin{cases} a-b, & \mbox{if } a \ge b \\ -(b-a), & \mbox{if } a < b. \end{cases}$

If the natural numbers are identified with the corresponding integers (using the embedding mentioned above), this convention creates no ambiguity.^{[citation needed]}

This notation recovers the familiar representation of the integers as {... −3,−2,−1, 0, 1, 2, 3, ...}.

Some examples are:

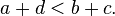
$\begin{align} 0 &= [(0,0)] &= [(1,1)] &= \cdots & &= [(k,k)] \\ 1 &= [(1,0)] &= [(2,1)] &= \cdots & &= [(k+1,k)] \\-1 &= [(0,1)] &= [(1,2)] &= \cdots & &= [(k,k+1)] \\ 2 &= [(2,0)] &= [(3,1)] &= \cdots & &= [(k+2,k)] \\-2 &= [(0,2)] &= [(1,3)] &= \cdots & &= [(k,k+2)].\end{align}$

Thaqnks when I seen this I thought it looked more like algebra too complication for me, thanks for explaining it.

http://www.lotterypost.com/thread/233413 Popular numbers

12345

67890

Use Mirror #'s Use prs. with your Key* numbers the most Vivid thing in your dream go up or down on #'s. Flip 6=9 `9=6 Bullseyes 0 or 1 for Pick 4 and the P. 5 Play the other part of doubles. Do the Whole nine yards for a P. 4* P. 5* or 0 thur 9 for P. 4 P. 5 from my dreams or hunches good Luck.. Write your Dreams down Play for 3 days. Good Luck All.

NetConnect

Internet Domains, simple and cheap

Find a domain name:

Is AnyOne Good with Integers!!