Suppose you're a juror on a homicide case. There's really no tangible evidence of any connection between the victim and the defendant other than a DNA match. Suppose the law enforcement investigators did a nationwide DNA database search and matched the defendant, and the prosecutor brought the case stating that there's a 1 in 10 million random probability of a match based on the specific DNA markers. Nobody else in the DNA dragnet was a match. Would you convict the defendant?
Perhaps there are 30 million people in the U.S. databases, for the sake of argument. Another 50 million people can be eliminated due to age other circumstances. That leaves 250 million people that might, hypothetically, be a match, as their DNA data is not available. Let's say that based on the circumstances of the case, there's an extremely high likelihood that someone with a DNA match perpetrated the crime. Let's assume that a DNA match person did it. What's the probability that the defendant perpetrated the crime?
You might come back with the response "Easy, it's just 1 in 25". You get that by multiplying the probability of an individual match by the population size. With 1 in 10 million probability per individual and a potential population pool of 250 million people, that's, on average, there are 25 matches. The defendant is one of them, so statistically he is one of 25 people who might have been the perpetrator. In this case, with the numbers I gave, that's very nearly the actual answer. What we're actually doing here is using a Normal distribution approximation of the Binomial Distribution (which is the exact calculation method). The Normal approximation works if np ∼ 5 or greater. We were lucky we met the criterion in this instance.
What if, instead, the random probability is 1 in 100 million or 1 in a billion? We can't accurately use the Normal approximation anymore. We need to do the direct Binomial calculation. (A Poisson calculation might be very close, much better than Normal, but Binomial is exact.) What's the formula for probability that the defendant is guilty?
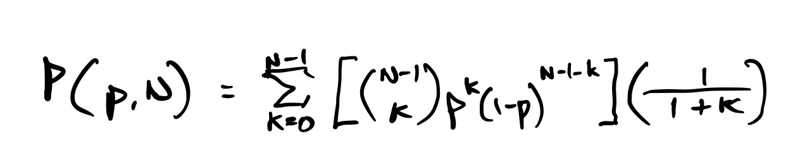
p is the probability of one individual being a being a random match, e.g. 1 in 10 million, 100 million, 1 billion, etc. N is the population from which the guilty party may be drawn, in our example, 250 million. Let's now try p = 1 in 100 million and N = 250 million. Then,
P(p=1/100M, N=250M) = 0.367
P(p=1/1B, N=250M) = 0.884
Even in the latter case, would you convict on that probability, absent other meaningful evidence?
Let's now make the issue a lot murkier. Say the victim and the defendant lived in the same large metropolitan area of 5 million people (after eliminating young children and others who without a doubt could not have done it). The prosecutor might argue, to get his numbers up, we need to narrow the possible population pool to 5 million. That's a tough one, as anybody passing through may have done it too. Let's humor the prosecutor and do the calculations.
P(p=1/10M, N=5M) = 0.787
P(p=1/100M, N=5M) = 0.975
P(p=1/1B, N=5M) = 0.998
I wonder how many people would put someone in prison for a very long time with a 2.5% probability of innocence or a 0.2% probability of innocence. Hard to know, but interesting to ponder. Of course, this is making the very big assumption the jurors understand the mathematics. I think this demonstrates that "reasonable doubt" is a highly subjective concept even when you can calculate hypothetical statistical frequencies, and assuming the jury understands the numbers.