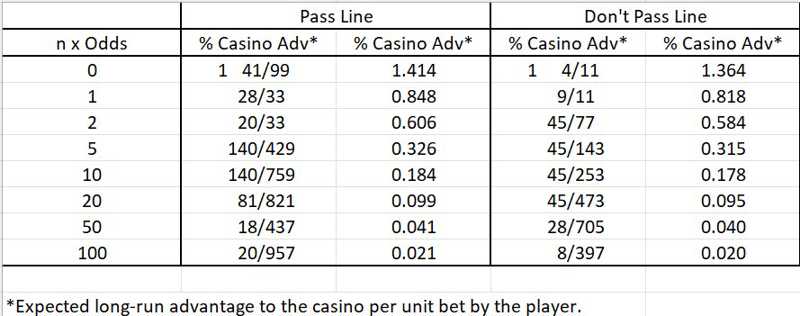
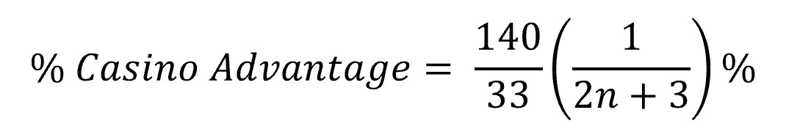Yes, the "odds" bet, sometimes called "free odds", is universally paid according to the true probabilities, without house advantage. However, before making this bet, you must make the Pass Line bet first, and that has a 1.414% house advantage. The casinos vary in how much you can bet on the "odds" as a multiplier of the original Pass Line bet. For example, a casino that offers 10x Odds on a $10 Pass Line bet will let you bet up to $100 on the "odds" bet.
As an example of how "odds" or "free odds" function, consider the basics of the Pass Line first. Two six-sided dice are rolled, and the total is summed. A result of 2, 3, or 12 means you immediately lose your Pass Line bet. A result of 7 or 11 means you win, and you are paid at even money, so for a $10 bet, for example, you will be returned your $10 bet + $10 winnings. Any other result is called a "point". The way the "point" works is that the dice are continued to be rolled in succession until either the "point" is rolled or a 7. If the "point" occurs, you win and are paid at even money. If a 7 occurs before the "point", then the House wins, and the bet is lost.
Enter "odds"/"free odds". As mentioned, this bet can only be made when the Pass Line bet is made first. Also, crucially, it is only possible when a "point" is established. Let's say, for example, the "point" is 4, and the House allows 10x odds on a $10 pass line bet. You can then make a (side/additional) $100 "odds" bet over and above the original $10 Pass Line. If, after additional rolls, 4 occurs before a 7, then you win both the original Pass Line bet as well as the "odds" bet. Because 7 is twice as likely to occur as 4, you are paid at 2 to 1 on a winning "odds" bet, proportional to the true probability. (If 7 occurs first, you lose both the Pass Line bet and the "Odds" bet.) In my example, assuming 4 is rolled before a 7, the $100 (10x) "odds" bet would result in $200 winnings, and that is in addition to the even-money win of $10 on the original $10 Pass Line. The total winnings would be $210 on $110 at risk.