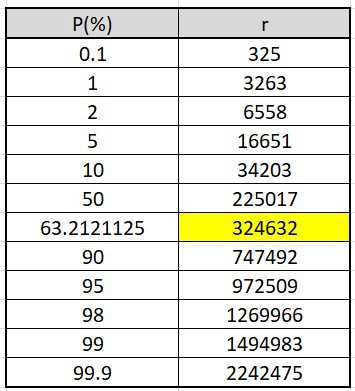
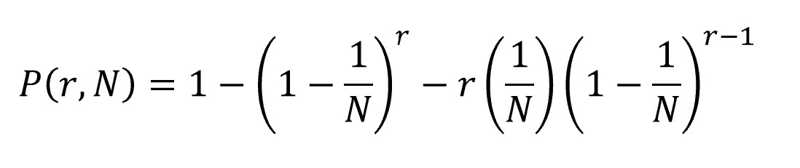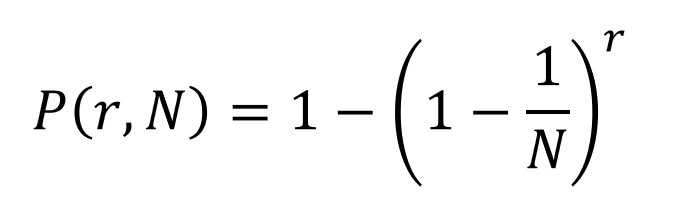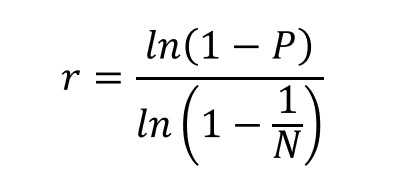While there's no guarantee that there will be a certain number of repeats, the probability of it happening at least once in 8000 draws (for a 5/35 game) is 99.999...% or very nearly 100%.
To see why, start with a small example with a simpler game. What is the likelihood of no repeats in Pick 3 played straight, over a period of 2 consecutive games? That would be just 999/1000, and so the probability of a repeat is 1 - 999/1000 = 1/1000 = 0.1%.
The likelihood of no repeats in Pick 3 played straight, over a period of 3 consecutive games is (999/1000) x (998/1000), so the probability of at least one repeat is 1 - (999/1000)(998/1000) ≈ 0.3%. Getting a little more likely to see a repeat.
The likelihood of no repeats in Pick 3 played straight, over a period of 4 consecutive games is (999/1000) x (998/1000) x (997/1000), so the probability of at least one repeat is 1 - (999/1000)x(998/1000)(997/1000) ≈ 0.6%.
The likelihood of no repeats in Pick 3 played straight, over a period of 20 consecutive games is (999/1000) x (998/1000) x (997/1000) x ... x (981/1000), so the probability of at least one repeat is 1 - (999/1000)x(998/1000)x(997/1000)x...x(981/1000) ≈ 17.4%.
The likelihood of no repeats in Pick 3 played straight, over a period of 50 consecutive games is (999/1000) x (998/1000) x (997/1000) x ... x (951/1000), so the probability of at least one repeat is 1 - (999/1000)x(998/1000)x(997/1000)x...x(951/1000) ≈ 71.2%.
The more consecutive games you analyze, assuming each game's outcome is independent of the previous, the more likely it is you see at least one repeat. To analyze a different game with more combos, it's a simple change of numerators and denominators. For CT Cash 5 over a period of 8000 games, the number you're looking at is
1 - (324631/324632)x(324630/324632)x(324629/324632)x...x(316631/324632) = 99.9999999...%
There's a practically 100% chance you'll see a repeat in CT Cash 5 over that many draws.