The weak law
The weak law of large numbers states that if X1, X2, X3, ... is an infinite sequence of random variables, where all the random variables have the same expected value μ and variance σ2; and are uncorrelated (i.e., the correlation between any two of them is zero), then the sample average

converges in probability to μ. Somewhat less tersely: For any positive number ε, no matter how small, we have

[edit]
Proof
Chebyshev's inequality is used to prove this result. Finite variance  (for all i) and no correlation yield that
(for all i) and no correlation yield that

The common mean μ of the sequence is the mean of the sample average:

Using Chebyshev's inequality on 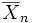 results in
results in

This may be used to obtain the following:

As n approaches infinity, the expression approaches 1.
Proof ends here
The result holds also for the 'infinite variance' case, provided the Xi are mutually independent and their (finite) mean μ exists.
A consequence of the weak law of large numbers is the asymptotic equipartition property.
[edit]
The strong law
The strong law of large numbers states that if X1, X2, X3, ... is an infinite sequence of random variables that are pairwise independent and identically distributed with E(|Xi|) < ∞ (and where the common expected value is μ), then

i.e., the sample average converges almost surely to μ.
If we replace the finite expectation condition with a finite second moment condition, E(Xi2) < ∞ (which is the same as assuming that Xi has variance), then we obtain both almost sure convergence and convergence in mean square. In either case, these conditions also imply the consequent weak law of large numbers, since almost sure convergence implies convergence in probability (as, indeed, does convergence in mean square).
This law justifies the intuitive interpretation of the expected value of a random variable as the "long-term average when sampling repeatedly".
[edit]
A weaker law and proof
Proofs of the above weak and strong laws of large numbers are rather involved. The consequent of the slightly weaker form below is implied by the weak law above (since convergence in distribution is implied by convergence in probability), but has a simpler proof.
Theorem. Let X1, X2, X3, ... be a sequence of random variables, independent and identically distributed with common mean μ < ∞, and define the partial sum Sn := X1 + X2 + ... +Xn. Then, Sn / n converges in distribution to μ.
Proof. (See [1], p. 174) By Taylor's theorem for complex functions, the characteristic function of any random variable, X, with finite mean μ, can be written as

Then, since the characteristic function of the sum of independent random variables is the product of their characteristic functions, the characteristic function of Sn / n is
![\left[\varphi\left({t \over n}\right)\right]^n = \left[1 + i\mu{t \over n} + o\left({t \over n}\right)\right]^n \, \rightarrow \, e^{it\mu}, \quad \textrm{as} \quad n \rightarrow \infty.](http://upload.wikimedia.org/math/7/3/d/73d2452ad3dbd2df80b4f3606af38442.png)
The limit eitμ is the characteristic function of the constant random variable μ, and hence by the Lévy continuity theorem, Sn / n converges in distribution to μ. Note that the proof of the central limit theorem, which tells us more about the convergence of the average to μ (when the variance σ 2 is finite), follows a very similar approach.
[edit]
References
- Grimmett, G. R. and Stirzaker, D. R. (1992). Probability and Random Processes, 2nd Edition. Clarendon Press, Oxford. ISBN 0-19-853665-8.
[edit]
See also
[edit]
External links
- MathWorld: Weak Law of Large Numbers
- MathWorld: Strong Law of Large Numbers
Retrieved from "http://en.wikipedia.org/wiki/Law_of_large_numbers"
Category: Probability theory



