- Home
- Premium Memberships
- Lottery Results
- Forums
- Predictions
- Lottery Post Videos
- News
- Search Drawings
- Search Lottery Post
- Lottery Systems
- Lottery Charts
- Lottery Wheels
- Worldwide Jackpots
- Quick Picks
- On This Day in History
- Blogs
- Online Games
- Premium Features
- Contact Us
- Whitelist Lottery Post
- Rules
- Lottery Book Store
- Lottery Post Gift Shop

The time is now 11:23 pm
You last visited
April 23, 2024, 9:46 pm
All times shown are
Eastern Time (GMT-5:00)

What's next?Prev TopicNext Topic
-
 Philadelpia/Pennsylvania
Philadelpia/Pennsylvania
United States
Member #2,218
September 1, 2003
6,802 Posts
OfflineQuote: Originally posted by bobby623 on Jul 11, 2013
Greenfox
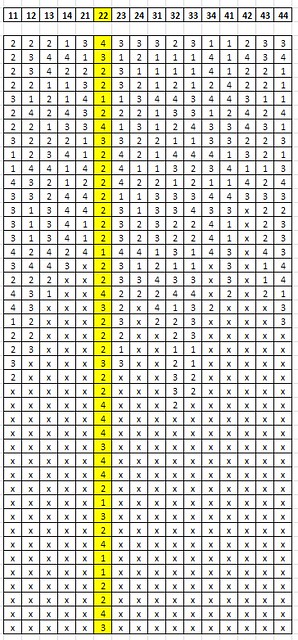
Here the complete and updated Pair chart.
Note that Pair 22 is leading the pack!11 12 13 14 21 22 23 24 31 32 33 34 41 42 43 44
2 2 2 1 3 4 3 3 3 2 31 1 2 3 3
2 3 4 4 1 3 1 2 1 1 1 4 1 4 34
2 3 4 2 2 2 3 1 1 1 1 4 1 2 2 1
2 2 1 1 3 2 3 2 1 2 1 2 4 2 2 1
3 1 2 1 4 1 1 3 4 4 3 4 4 3 1 1
2 4 2 4 3 2 2 2 1 3 3 1 2 4 2 4
2213 3413 1243 3431
3222 1332 2113 3223
1234 1242 1444 1321
1441 4241 1323 4113
4321 2242 2121 1424
3324 4211 3334 4333
3134 4231 3343 3x22
3134 1232 3224 1x23
3134 1232 3224 1x23
4242 4144 1314 3x43
3443 x231 211x 3x14
222x x233 433x 3x14
431x x422 244x 2x21
43xx x32x 413 2xx3
12xx x23x 223x xxx3
22xx x22x x23x xxxx
23xx x21x x11x xxxx
3xxx x33x x21x xxxx
2xxx x2xx x32x xxxx
xxxx x2xx x32x xxxx
xxxx x4xx x2xx xxxx
xxxx x4xx xxxx xxxx
xxxx x4xx xxxx xxxx
xxxx x3xx xxxx xxxx
xxxx x4xx xxxx xxxx
xxxx x4xx xxxx xxxx
xxxx x2xx xxxx xxxx
xxxx x1xx xxxx xxxx
xxxx x3xx xxxx xxxx
xxxx x2xx xxxx xxxx
xxxx x4xx xxxx xxxx
xxxx x1xx xxxx xxxx
xxxx x1xx xxxx xxxx
xxxx x2xx xxxx xxxx
xxxx x2xx xxxx xxxx
xxxx x4xx xxxx xxxx
xxxx x3xx xxxx xxxx
Sorry about the alignment. Not good at formatting on PC!!Hope this confirms your ideas.
Thanks again
Bobby
-
 Philadelpia/Pennsylvania
Philadelpia/Pennsylvania
United States
Member #2,218
September 1, 2003
6,802 Posts
OfflineI updated the Excel files.
Here is the download link to all the files:
https://app.box.com/s/lasyla0zz3edprvm3l27
The only 3 files you need are TexasPick3V3, BookD, and BookDPart2
-
 Philadelpia/Pennsylvania
Philadelpia/Pennsylvania
United States
Member #2,218
September 1, 2003
6,802 Posts
OfflineI updated the Excel files and also created 2 additional Excel files for "Pairs" both Alpha and Numerical ("F" String).
The charts will calculate the "next" single Alpha or Digit depending on what Excel file you have opened.
There is a Totals for what Alpha / Digit followed.
Here is the link to the Youtube video with a better explanation. The video also pertains to the Alpha Pairs Excel file also.
http://www.youtube.com/watch?v=RP-cPEIg3Xw
The Excel files were updated at 2:30 Eastern Time
-
bobby623 and winsum,
Here is what I came up with for this. I know that winsum has most of this already programmed, but I told bobby I'd look at it for him and see what I could come with. You may be able to incorporate it into what you have already and it may just be as useless as I am.
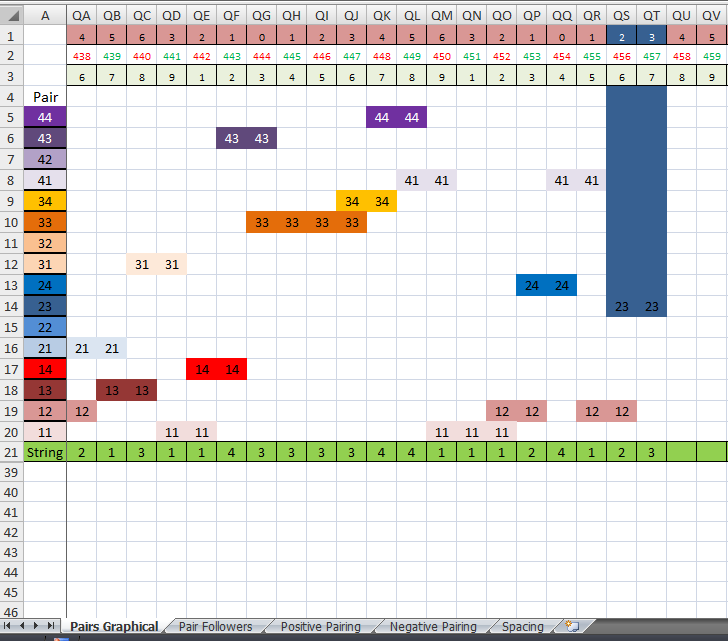
There are 5 sheets in the book. Each doing something different, but all serving the same purpose. This is the only sheet that need anything filled out in it to take care of the rest. You just have to put the digit string in row 21 as it comes in, and it will fill in all the other sheets for you. This is the pair graphical sheet and the first sheet in the book. All this one does is it pops up the pairs as they come along so the eyes can see them as they are. It is set up right now for 1,373 digits in a string and just needs dragged over if more is needed. It starts with where he put me at in his string in column F as the first digit in the string and carries on to the right. I'm not sure where he is now in it. Column A shows you the pairs and is froze so it will stay in view when scrolling to see the others. B will count the amount of times that each pair comes up in the string. D gives the percentage that each does so. D21 will be the amount of digits in the string in total. Each pair has it's own color code and each page is set up the same way as this as far as where the pairs are so no one gets confused. This probably won't get used by anyone, but I tried to keep it as simple as I could to read.
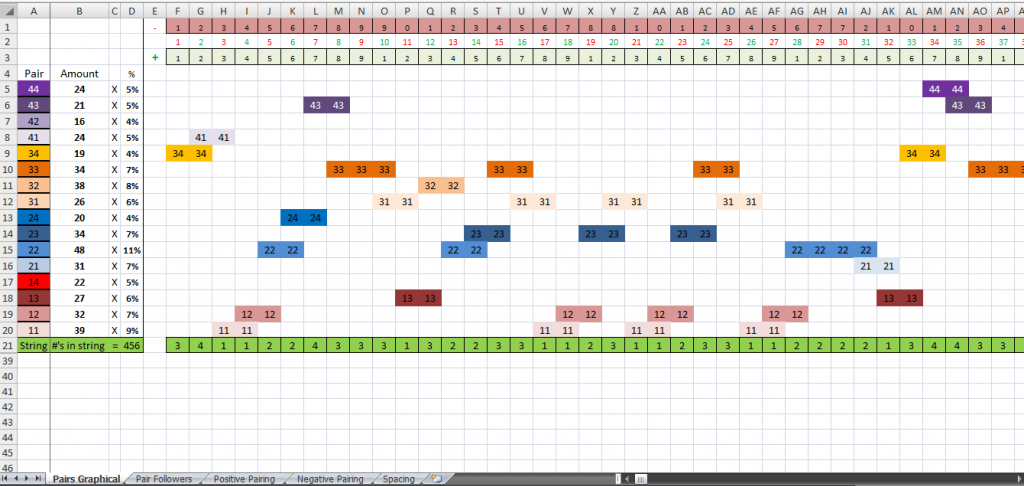
With this type of workout, you are looking for what comes next to help pick what to play. Right off the bat, your knowing where the last set left off. It was 12. So you know that the next pair is going to and has to be either 21,22,23, or 24. After that pair, it has to be either 21,22,23,24 again if cell QT21 is a 2. If QT21 is a 3, then the next pair has to be either 31,32,33 or 34 for he next pair. And so on with the 1 and 4. At the end of every string it leaves you with the front of the next pair that is coming. So your going to need to know how to find what is going to be in QT21 coming next, then you'll be on your way to what is going to be in QU21. Then from QU21 you'll be started on QV21 and so on.

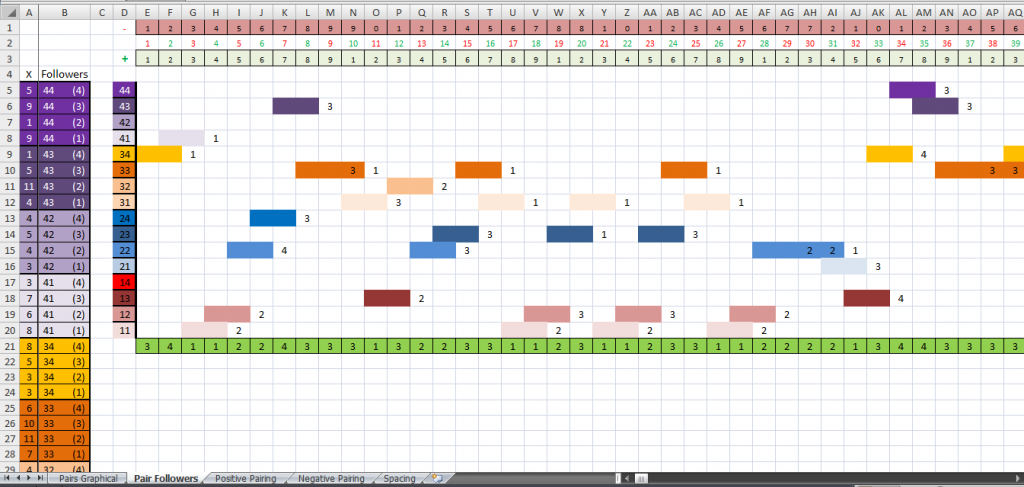
This is the next sheet in the book. I know winsum has something similar to this to. Both do the same thing. All it does is color codes your pairs for you and shows you what came next. Just simple straight forwardness here. Again, column A is locked so you can scroll to the right and keep what happened in view. A will show you how many times tha each pair is followed by what number. B will show you the pairs and what number followed it. Cell A5 would mean that pair 44 was followed by 4 an amount of 5 times as an example. There are a few times on this set of string that a number was followed by a certain digit quite a few times more than the others. Like with the 43 pair and it being followed by 2 the most at 11 times. There are the ones that have a similar amount of follower amounts like the 42 pair. There isn't much to tell there, but with the 43 pair, I'd keep the 2 follower as my top choice for what's next simply because it has been a follower at least 6 more times than the next highest amount of 5, which would be the 3 follower. With what I've seen with all he work I've done on these games, if something happens a larger amount of times, then there is a reason. May not know exactly what that reason is, but has to be a reason.Since the last pair showing in the string was 12, I looked at it's followers and see that 12 was followed by 1,2 and 3 all an amount of 9 times each with 4 coming in at 4 times. So not much to really go on there.
This is the Positive pairing sheet. Sheet 3 in the book. Again, A is froze so the pairs are visible throughout. Keeping pair 44 as the largest at the top. What I've been looking at with this sheet, (and the next sheet coming up), is like a matching game. If you look at row 2, that is a counter row. It counts how many digits are in the string. Just simplicity there. It starts with 1 and not 0. 0 is nothing, with 1 being the first. Row 1 is if you took what digits are in row 2, and subtracted the smallest digit from the largest. (Once you get up into the double, triple and quad numbers). Row 3 is the single added sum of row 2. Nothing fancy at all. This being the positive pairing sheet, I was looking for a single sum of each pair, and comparing it to how many times it may or may not show up with the corresponding column in row 3. Like the sum of pair 43 is 7. In J2 the counter is 7. 43 or 34 is the only possibilities that can total 7 the way this is set up. If you look on over in row 6 at the next time pair 43 came up, it was right after a 7 counter. So if I was closing in with a 7 as the counter in row 3, and had either 4 or 3 as the last digit in my string I'd look at the sum of 7 showing me either 43 for my pair coming, if the last digit was 4, or 34 if the last was 3. So far I have been seeing the sums matching up either right at, directly before or directly after. Sometimes you have to look at the numbers though to see wht I'm talking about. Like the quad 4's, or 44,44,44 triple pair in row 15. With that string, I'm probably either going to lose some of who read this, your going to think I'm crazier than you already do, you'll get what I'm talking about or it will just be completely wrong. This is just how my brain is interpreting it. Take the 6's in row 10. 6 is the sum of 33. 0 is the subtracted sum of 33. I already showed this I believe, but going to do it again in case I missed something. The first pair of 33 showed up on counter 8. (Column K). It went 33, 33 pairing up twice. Your working with single digits here for counters. You have an 8 either added or subtracted. 8+8=16. 16 is the sixth digit over in the teens just as 6 is the sixth digit over in the whole numbers. Then you have 9, which is the negative version of 6. 9+9=18 which totals 1+8=9. The opposite of 6. The it's followed by 10. Now 10 is either 0-1=9 (10-1=9). Either way you want to look at it. Or if 0 and 5 are opposites, then you have 10 = 15, and 1+5=6. There is 6,6,6 in three cells. That's three 6's which is two sets of 33 pair. If you go on over to column R where the next pairing of 33 showed up, your on counter 15 which is 1+5=6, and 16 and the sixth digit over in the teens just as 6 is the sixth digit over in the wholes. Next pairing of 33, sum of 6, is in AA10 and AB10. Which are 24 and 25 counters. The 24 is 2+4=6 and 25 is 2+5=7. 25 is also 3 subtracted. Here is where it starts getting confusing. And again, this is just how I'm looking at this. Might not be any help to anyone. With that 25 and it's 3 and 7 sums, you get 3+7=10 or 15, which is 1+5=6. You can also look at it as 25 as 20. Looking at it as 20, you have to see how the 0 effects numbers. Let's say that 0 halves a number. If it can do that, then you have half of 2 which is 1, (1 being the negative version of 2), coupled with that 0 or (5), you get 1+5=6 there. If you look at 2 and 0 as 2 being the second digit over in the whole numbers, and 12 as the second digit over in the doubles, and you half 12 because of the 0, or 5 (which is half), then you get 6. So you have 6 and 6 side by side there. Don't know if that makes a bit of sense to anyone or not. Just how I'm looking at it. And you can look at the next sets of 33 pairs coming in line there. Starting on 36, ending on 39. Let's look at the 34 and 43 pairs for a second. the second showing of pair 34 came in on the front side of counter 34, starting in 33 (AJ2) and ending on 34 (AK2). The 44 pair came off of the 34 pair, then went right in to the 43 pair on the back side, or reverse side of 34. Again, not sure if that makes any sense what so ever. Just calling it like I see it with this and throwing out ideas.
Anyway, that's what this sheet does. It will tell you how many times that every pair shows up on every counter. Some will be a higher amount of times, some are about even. Not many are even though.

Above shows the counter and where 44 pair showed up on each. Below are some more examples of what happened. 44 is either 0 or 8 for sums. The 44 pair showed up on the 4 counter the most with 6 times in this set of string. (Right before the halfway point of 5). Isn't 4 right before the halfway point in the whole digits?
The next set, same sheet with pairs 43 and 42. 43 came in on counter 3 the most with 5 times. Which isn't saying much. I'm still looking at this and going over it. But 4+3=7. I was looking for the 43 to come in on exactly a 7 counter the most, but it was second most on 7. 7 is the third digit backwards from 10, while 3 is the third digit forward from 0. There is a 3 in 43, and they are kind of reversed in order the way they make 7.
Under the 43 pair is 42. Same sheet, further down. I was looking for it to show up on counter 6 sums the most, but it was right before the 6. At the halfway point of 5. 2 is half of 4. What's funny to me about this one is the subtracted pairs sheet. For pair 42, the counter it came in on most was 1. 2 is half of 4 and 1 is half of 2. How many times did it show up on counter 1? 5 (or half times).
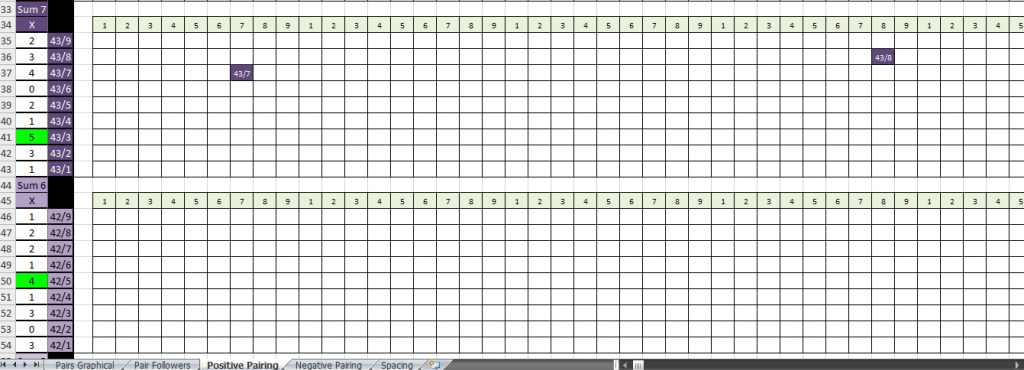
Here is further down showing the results of pairs 41 and 34. The 41 came in on 6 as the most. Right after the half way point of 5. I was hoping for 5 to be the counter it started on the most, but it was after that one with the 6. The amounts on the 41 pairs here look funny to me with all the 4's and 1's. (41), and the only differences was 3 and 5 totals. Both sums of 41. HMMM. Weird. Especially with the 4's all coming in on the first half of them and the only time that 41 came 1 time in those was on counter 4. May be nothing, but really looks odd to me about that. There was something else I saw with this, but got distracted by a squirrell running around out here. It'll come back to me.
With the 34 pair, again, I was looking at 7 wanting it to be the most. But again not. It was actually a tie for 3 times each on 3,4 and the 6. 6 being right before the 7. Kind of funny again on this one to. The 3 and 4 counters both had 3 times, with the other being the digit right before the 7 with the 6. 3 being half of 6, and 4 having a root of 2. Again, may be nothing. Just ideas.
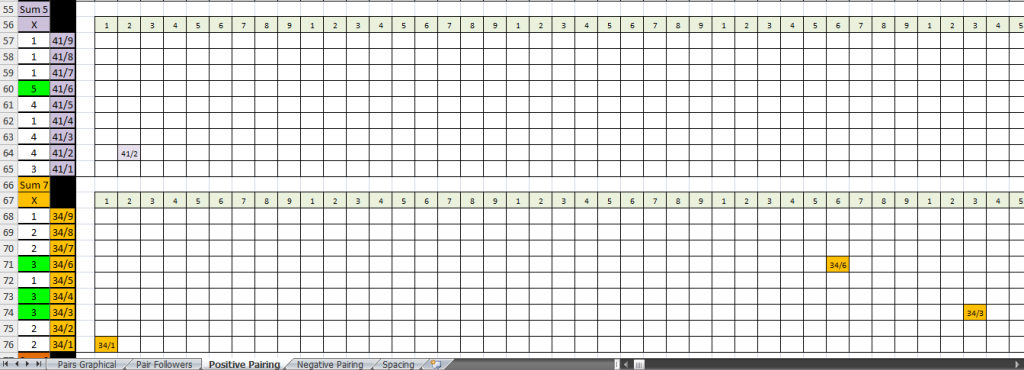
As for the possibilities of what's next after that 12 pair. It would have to be either 21, 22, 23 or 24. With what the totals for those pairs where, it could be either 22 or 23 with the counters being on 6 on the positive side. Both had a total of 5 times starting when the counter was 6. 22 started the most on counter 4 with 10 times. (Which was what I was hoping for). 23 started on 5 the most with 7 times. (Again, what I was hoping for). So with those possibilites, I'm looking at either 22 or 23 to be the pair that branches off of the 12 at the end of the string.
This is the fourth sheet of the book and is th same as above, only it compares negative sums of the pairs to the negative sums of the counters. This one shows the results of the 44 pair and it's 0 sum compared to row 1 subtracted sums. It started the most on counter 1, which is right after counter 0. There is no counter 0 on the positive sheet. If there are any numbers that will add together to give a sum of 0, I don't know of them. You can get 10, which is at the end of the spectrum, and kind of the same as 0, but 10 is that many more than 0. So, 0 is only factored in on this sheet for that reason. You can get 0 from 11, 22, 33 and so on. Subtracting. It still has to start counting on 1 though to be correct, so it does that. Also, this is formatted so that if you scroll down and don't know where you are on the counters, you can look in the rows of pink, like row 23, and the cell you are looking for will be golden. So you know where you are. Both this sheet and the positive pairing sheet are the same with that.

The 43 and 42 pair. Each of these sheets will go thru all pairs by scrolling down. Notice the placement of what took place on these. The 44 an even number and the counter it started on the most was 1, the digit right after it's subtracted sum. The 43 is odd, added is odd, and it started the most on 1 which was it's subtracted sum. Then the 42 an even number started on 1 the most with 2 being it's subtracted sum. It started the most on the counter that was right before it's sum. You'll see that quite a bit on these. I'll put the link on here for this book so anyone wanting to look it over can get it.
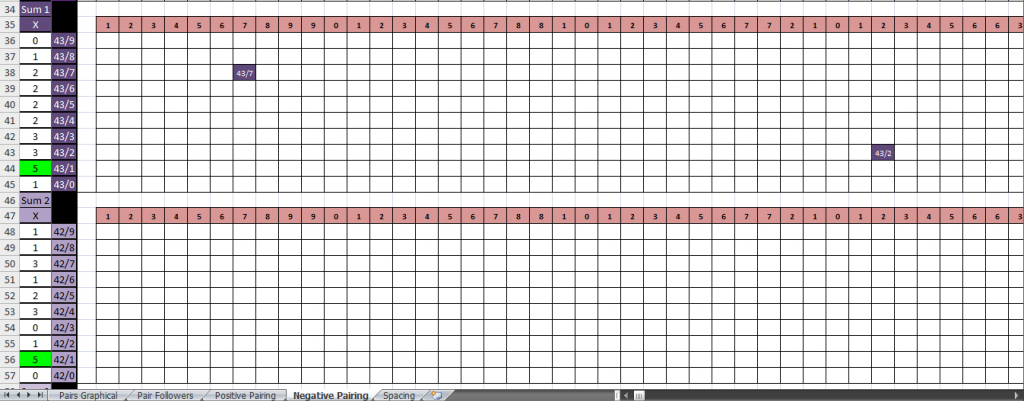
With the pairs of 41 and 34 further down on the same sheet. 41 started on counter 2 the most, right before it's subtracted sum. With counters 0 and 3 being second most. 0 is positive of 5. 5 is the added sum of 41, 3 is the subtracted sum.
34 started on 0 the most. The number right before the subtracted sum of 34, 1. With that 1 counter along with the 4 counter coming in second most with 4 a piece.
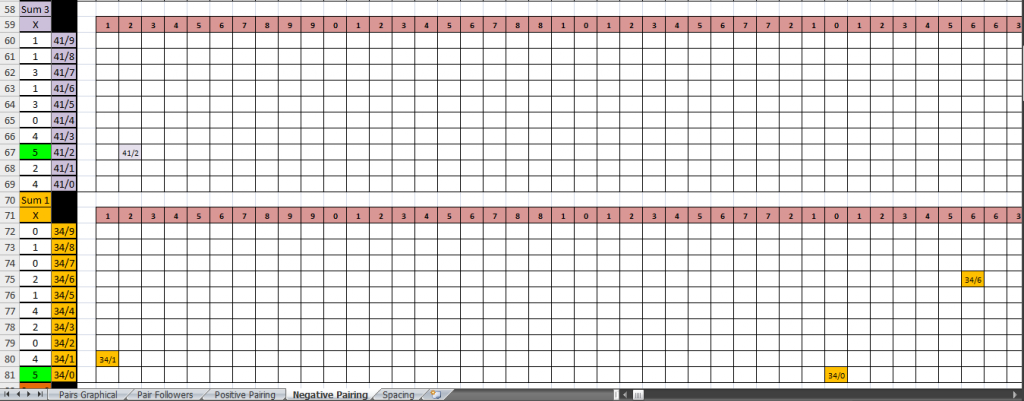
Still looking for what pair will branch off of that 12 that's hanging on the end there. Both the 22 and 23 pair again have started the most on negative counter 2. Both with 7 times each.
The last, 5th sheet of this, is what I have shown on here. It's the spacing between each time the pairs show up. It has the amount of space between each pair, shows the largest amount of space that has occurred, and breaks those amounts into their whole number sums, incase there is something that that can be used for. Not going to put it on here again. But it's on the book and anyone interested can DL it and check it out.
So back to what's next after that 12. It had to be either 21, 22, 23 or 24 that branched off the 2 from that 12. Using the counters to get an idea I narrowed it down to two out of 4. (May not be right, because I don't know what came after that yet). But was looking for either 22 or 23 to be next in line. Here is both the 2 for 22 and 3 for 23 put in to the string so you can see what it looks like and see if one fit better than the other.
With the 22 being next pair.

With the 23 being next pair.
And that's about all the time I got right now. I gotta eat something.
Here is the book link. https://www.dropbox.com/s/g6vjtl966p1a0az/bobby623.xlsx
It has everything I've shown here.
Winsum, I made a couple changes on this one that the one I sent you doesn't have. It's just on the followers sheet is all. I turned around the 1,2,3,4 for each pair and put them 4,3,2,1 from top to bottom. To kind of keep them like the rest of the layout. If there is something you might find useful on it and can use or incorporate into what you have, feel free to do with it what you want.
You can't steal second and keep your foot on FIRST!!!
“Strength does not come from winning. Your struggles develop your strengths.
When you go through hardships and decide not to surrender, that is strength”.-Arnold (Ahnald) Schwarzenegger-
-
Quote: Originally posted by Greenfox on Sep 7, 2013
bobby623 and winsum,
Here is what I came up with for this. I know that winsum has most of this already programmed, but I told bobby I'd look at it for him and see what I could come with. You may be able to incorporate it into what you have already and it may just be as useless as I am.
There are 5 sheets in the book. Each doing something different, but all serving the same purpose. This is the only sheet that need anything filled out in it to take care of the rest. You just have to put the digit string in row 21 as it comes in, and it will fill in all the other sheets for you. This is the pair graphical sheet and the first sheet in the book. All this one does is it pops up the pairs as they come along so the eyes can see them as they are. It is set up right now for 1,373 digits in a string and just needs dragged over if more is needed. It starts with where he put me at in his string in column F as the first digit in the string and carries on to the right. I'm not sure where he is now in it. Column A shows you the pairs and is froze so it will stay in view when scrolling to see the others. B will count the amount of times that each pair comes up in the string. D gives the percentage that each does so. D21 will be the amount of digits in the string in total. Each pair has it's own color code and each page is set up the same way as this as far as where the pairs are so no one gets confused. This probably won't get used by anyone, but I tried to keep it as simple as I could to read.

With this type of workout, you are looking for what comes next to help pick what to play. Right off the bat, your knowing where the last set left off. It was 12. So you know that the next pair is going to and has to be either 21,22,23, or 24. After that pair, it has to be either 21,22,23,24 again if cell QT21 is a 2. If QT21 is a 3, then the next pair has to be either 31,32,33 or 34 for he next pair. And so on with the 1 and 4. At the end of every string it leaves you with the front of the next pair that is coming. So your going to need to know how to find what is going to be in QT21 coming next, then you'll be on your way to what is going to be in QU21. Then from QU21 you'll be started on QV21 and so on.

This is the next sheet in the book. I know winsum has something similar to this to. Both do the same thing. All it does is color codes your pairs for you and shows you what came next. Just simple straight forwardness here. Again, column A is locked so you can scroll to the right and keep what happened in view. A will show you how many times tha each pair is followed by what number. B will show you the pairs and what number followed it. Cell A5 would mean that pair 44 was followed by 4 an amount of 5 times as an example. There are a few times on this set of string that a number was followed by a certain digit quite a few times more than the others. Like with the 43 pair and it being followed by 2 the most at 11 times. There are the ones that have a similar amount of follower amounts like the 42 pair. There isn't much to tell there, but with the 43 pair, I'd keep the 2 follower as my top choice for what's next simply because it has been a follower at least 6 more times than the next highest amount of 5, which would be the 3 follower. With what I've seen with all he work I've done on these games, if something happens a larger amount of times, then there is a reason. May not know exactly what that reason is, but has to be a reason.Since the last pair showing in the string was 12, I looked at it's followers and see that 12 was followed by 1,2 and 3 all an amount of 9 times each with 4 coming in at 4 times. So not much to really go on there.

This is the Positive pairing sheet. Sheet 3 in the book. Again, A is froze so the pairs are visible throughout. Keeping pair 44 as the largest at the top. What I've been looking at with this sheet, (and the next sheet coming up), is like a matching game. If you look at row 2, that is a counter row. It counts how many digits are in the string. Just simplicity there. It starts with 1 and not 0. 0 is nothing, with 1 being the first. Row 1 is if you took what digits are in row 2, and subtracted the smallest digit from the largest. (Once you get up into the double, triple and quad numbers). Row 3 is the single added sum of row 2. Nothing fancy at all. This being the positive pairing sheet, I was looking for a single sum of each pair, and comparing it to how many times it may or may not show up with the corresponding column in row 3. Like the sum of pair 43 is 7. In J2 the counter is 7. 43 or 34 is the only possibilities that can total 7 the way this is set up. If you look on over in row 6 at the next time pair 43 came up, it was right after a 7 counter. So if I was closing in with a 7 as the counter in row 3, and had either 4 or 3 as the last digit in my string I'd look at the sum of 7 showing me either 43 for my pair coming, if the last digit was 4, or 34 if the last was 3. So far I have been seeing the sums matching up either right at, directly before or directly after. Sometimes you have to look at the numbers though to see wht I'm talking about. Like the quad 4's, or 44,44,44 triple pair in row 15. With that string, I'm probably either going to lose some of who read this, your going to think I'm crazier than you already do, you'll get what I'm talking about or it will just be completely wrong. This is just how my brain is interpreting it. Take the 6's in row 10. 6 is the sum of 33. 0 is the subtracted sum of 33. I already showed this I believe, but going to do it again in case I missed something. The first pair of 33 showed up on counter 8. (Column K). It went 33, 33 pairing up twice. Your working with single digits here for counters. You have an 8 either added or subtracted. 8+8=16. 16 is the sixth digit over in the teens just as 6 is the sixth digit over in the whole numbers. Then you have 9, which is the negative version of 6. 9+9=18 which totals 1+8=9. The opposite of 6. The it's followed by 10. Now 10 is either 0-1=9 (10-1=9). Either way you want to look at it. Or if 0 and 5 are opposites, then you have 10 = 15, and 1+5=6. There is 6,6,6 in three cells. That's three 6's which is two sets of 33 pair. If you go on over to column R where the next pairing of 33 showed up, your on counter 15 which is 1+5=6, and 16 and the sixth digit over in the teens just as 6 is the sixth digit over in the wholes. Next pairing of 33, sum of 6, is in AA10 and AB10. Which are 24 and 25 counters. The 24 is 2+4=6 and 25 is 2+5=7. 25 is also 3 subtracted. Here is where it starts getting confusing. And again, this is just how I'm looking at this. Might not be any help to anyone. With that 25 and it's 3 and 7 sums, you get 3+7=10 or 15, which is 1+5=6. You can also look at it as 25 as 20. Looking at it as 20, you have to see how the 0 effects numbers. Let's say that 0 halves a number. If it can do that, then you have half of 2 which is 1, (1 being the negative version of 2), coupled with that 0 or (5), you get 1+5=6 there. If you look at 2 and 0 as 2 being the second digit over in the whole numbers, and 12 as the second digit over in the doubles, and you half 12 because of the 0, or 5 (which is half), then you get 6. So you have 6 and 6 side by side there. Don't know if that makes a bit of sense to anyone or not. Just how I'm looking at it. And you can look at the next sets of 33 pairs coming in line there. Starting on 36, ending on 39. Let's look at the 34 and 43 pairs for a second. the second showing of pair 34 came in on the front side of counter 34, starting in 33 (AJ2) and ending on 34 (AK2). The 44 pair came off of the 34 pair, then went right in to the 43 pair on the back side, or reverse side of 34. Again, not sure if that makes any sense what so ever. Just calling it like I see it with this and throwing out ideas.
Anyway, that's what this sheet does. It will tell you how many times that every pair shows up on every counter. Some will be a higher amount of times, some are about even. Not many are even though.

Above shows the counter and where 44 pair showed up on each. Below are some more examples of what happened. 44 is either 0 or 8 for sums. The 44 pair showed up on the 4 counter the most with 6 times in this set of string. (Right before the halfway point of 5). Isn't 4 right before the halfway point in the whole digits?
The next set, same sheet with pairs 43 and 42. 43 came in on counter 3 the most with 5 times. Which isn't saying much. I'm still looking at this and going over it. But 4+3=7. I was looking for the 43 to come in on exactly a 7 counter the most, but it was second most on 7. 7 is the third digit backwards from 10, while 3 is the third digit forward from 0. There is a 3 in 43, and they are kind of reversed in order the way they make 7.
Under the 43 pair is 42. Same sheet, further down. I was looking for it to show up on counter 6 sums the most, but it was right before the 6. At the halfway point of 5. 2 is half of 4. What's funny to me about this one is the subtracted pairs sheet. For pair 42, the counter it came in on most was 1. 2 is half of 4 and 1 is half of 2. How many times did it show up on counter 1? 5 (or half times).

Here is further down showing the results of pairs 41 and 34. The 41 came in on 6 as the most. Right after the half way point of 5. I was hoping for 5 to be the counter it started on the most, but it was after that one with the 6. The amounts on the 41 pairs here look funny to me with all the 4's and 1's. (41), and the only differences was 3 and 5 totals. Both sums of 41. HMMM. Weird. Especially with the 4's all coming in on the first half of them and the only time that 41 came 1 time in those was on counter 4. May be nothing, but really looks odd to me about that. There was something else I saw with this, but got distracted by a squirrell running around out here. It'll come back to me.
With the 34 pair, again, I was looking at 7 wanting it to be the most. But again not. It was actually a tie for 3 times each on 3,4 and the 6. 6 being right before the 7. Kind of funny again on this one to. The 3 and 4 counters both had 3 times, with the other being the digit right before the 7 with the 6. 3 being half of 6, and 4 having a root of 2. Again, may be nothing. Just ideas.

As for the possibilities of what's next after that 12 pair. It would have to be either 21, 22, 23 or 24. With what the totals for those pairs where, it could be either 22 or 23 with the counters being on 6 on the positive side. Both had a total of 5 times starting when the counter was 6. 22 started the most on counter 4 with 10 times. (Which was what I was hoping for). 23 started on 5 the most with 7 times. (Again, what I was hoping for). So with those possibilites, I'm looking at either 22 or 23 to be the pair that branches off of the 12 at the end of the string.
This is the fourth sheet of the book and is th same as above, only it compares negative sums of the pairs to the negative sums of the counters. This one shows the results of the 44 pair and it's 0 sum compared to row 1 subtracted sums. It started the most on counter 1, which is right after counter 0. There is no counter 0 on the positive sheet. If there are any numbers that will add together to give a sum of 0, I don't know of them. You can get 10, which is at the end of the spectrum, and kind of the same as 0, but 10 is that many more than 0. So, 0 is only factored in on this sheet for that reason. You can get 0 from 11, 22, 33 and so on. Subtracting. It still has to start counting on 1 though to be correct, so it does that. Also, this is formatted so that if you scroll down and don't know where you are on the counters, you can look in the rows of pink, like row 23, and the cell you are looking for will be golden. So you know where you are. Both this sheet and the positive pairing sheet are the same with that.

The 43 and 42 pair. Each of these sheets will go thru all pairs by scrolling down. Notice the placement of what took place on these. The 44 an even number and the counter it started on the most was 1, the digit right after it's subtracted sum. The 43 is odd, added is odd, and it started the most on 1 which was it's subtracted sum. Then the 42 an even number started on 1 the most with 2 being it's subtracted sum. It started the most on the counter that was right before it's sum. You'll see that quite a bit on these. I'll put the link on here for this book so anyone wanting to look it over can get it.

With the pairs of 41 and 34 further down on the same sheet. 41 started on counter 2 the most, right before it's subtracted sum. With counters 0 and 3 being second most. 0 is positive of 5. 5 is the added sum of 41, 3 is the subtracted sum.
34 started on 0 the most. The number right before the subtracted sum of 34, 1. With that 1 counter along with the 4 counter coming in second most with 4 a piece.

Still looking for what pair will branch off of that 12 that's hanging on the end there. Both the 22 and 23 pair again have started the most on negative counter 2. Both with 7 times each.
The last, 5th sheet of this, is what I have shown on here. It's the spacing between each time the pairs show up. It has the amount of space between each pair, shows the largest amount of space that has occurred, and breaks those amounts into their whole number sums, incase there is something that that can be used for. Not going to put it on here again. But it's on the book and anyone interested can DL it and check it out.
So back to what's next after that 12. It had to be either 21, 22, 23 or 24 that branched off the 2 from that 12. Using the counters to get an idea I narrowed it down to two out of 4. (May not be right, because I don't know what came after that yet). But was looking for either 22 or 23 to be next in line. Here is both the 2 for 22 and 3 for 23 put in to the string so you can see what it looks like and see if one fit better than the other.
With the 22 being next pair.

With the 23 being next pair.

And that's about all the time I got right now. I gotta eat something.
Here is the book link. https://www.dropbox.com/s/g6vjtl966p1a0az/bobby623.xlsx
It has everything I've shown here.
Winsum, I made a couple changes on this one that the one I sent you doesn't have. It's just on the followers sheet is all. I turned around the 1,2,3,4 for each pair and put them 4,3,2,1 from top to bottom. To kind of keep them like the rest of the layout. If there is something you might find useful on it and can use or incorporate into what you have, feel free to do with it what you want.
Hi, Greenfox:
Great job! Both program and explanation are very clear!!!

But why I can not downloading your excel program above (I'm using Open Office)?
Thanks for your sincere sharing!!!
Best regards,
lb
- Saying Lotto #s Can be Predicted means that Lotto's ODD can be reduced down to an economical level by a system.
- Saying a Lotto System Works means that we can win constantly (not each draw) and economically (get a real profit) by using the System.
- Practice is the only criterion for testing truth.
-
Quote: Originally posted by lottoburg on Sep 7, 2013
Hi, Greenfox:
Great job! Both program and explanation are very clear!!!

But why I can not downloading your excel program above (I'm using Open Office)?
Thanks for your sincere sharing!!!
Best regards,
lb
Hi lottoburg and thanks!!!
I'm not sure what the problem is with the DL. I tried it and it worked fine here. It may be the open office as far as running it. I'm not sure. I tried the OO a while back and just didn't like the user interface at all with it. It should download fine, but I doubt that program will run it. I'm really not that familiar with it that much though, so I couldn't say for sure. If you don't have excel, there are the Kingsoft sheets that are about identical to excel. And it's a freeware program also. I know you can buy a version of it also that has more abilitites and it's about half the price of excel. Last I checked anyway. But you can set up the free version of it to run excel sheets. Another member found the Kingsoft and told me about them. I have both programs on my pc and there isn't a lot of difference from what I saw with them. It's a nice little program.
Your sure wlecome!!!
You can't steal second and keep your foot on FIRST!!!
“Strength does not come from winning. Your struggles develop your strengths.
When you go through hardships and decide not to surrender, that is strength”.-Arnold (Ahnald) Schwarzenegger-
-
Quote: Originally posted by Greenfox on Sep 11, 2013
Hi lottoburg and thanks!!!
I'm not sure what the problem is with the DL. I tried it and it worked fine here. It may be the open office as far as running it. I'm not sure. I tried the OO a while back and just didn't like the user interface at all with it. It should download fine, but I doubt that program will run it. I'm really not that familiar with it that much though, so I couldn't say for sure. If you don't have excel, there are the Kingsoft sheets that are about identical to excel. And it's a freeware program also. I know you can buy a version of it also that has more abilitites and it's about half the price of excel. Last I checked anyway. But you can set up the free version of it to run excel sheets. Another member found the Kingsoft and told me about them. I have both programs on my pc and there isn't a lot of difference from what I saw with them. It's a nice little program.
Your sure wlecome!!!
Hi, GreenFox:
You're right! The Kingsoft is working for your program now.
Thanks for sincere help and nice sharing!!!
Best regards,
lb
- Saying Lotto #s Can be Predicted means that Lotto's ODD can be reduced down to an economical level by a system.
- Saying a Lotto System Works means that we can win constantly (not each draw) and economically (get a real profit) by using the System.
- Practice is the only criterion for testing truth.


